El objetivo es mapear las coordenadas de un grid $(x, y)$ a un punto tridimensional: $P(x, y) = (x^{'}, y^{'}, z)$ de forma que transformando todos los puntos del grid consigamos un "océano" tridimensional.

Vamos a empezar por algo muy simple e iremos iterando paso a paso.
Por el carácter ondulatorio del océano tiene sentido intentar aproximarlo, al menos como primer intento, con funciones ondulatorias: senos y cosenos.
Algo así:
$$P(x, y) = (x, y, sin(x))$$
Veamos cómo.
Domando el seno
La función seno tiene la siguiente pinta:

Es una función periódica; se repite cada ciertos intervalos. En el caso del seno la función se repite con un periodo de $2\pi$. Matemáticamente:
$$sin(x) = sin(x + 2\pi) = sin(x + 4\pi) = sin(x + 6\pi), ...$$
En general,
$$sin(x) = sin(x + 2k\pi)$$
Al periodo también se le denomina longitud de onda (wavelength) ya que es la distancia entre crestas.
Quizás en muchos casos no sea útil tener el periodo en $2\pi$. ¿Podemos cambiar el periodo/wavelength de la función seno? Sí, podemos cambiar su periodo original $2\pi$ a uno nuevo $L$. Bastaría con remapear la entrada $x$ a:
$$sin(\frac{2\pi}{L}x)$$
La salida del seno está acotada en el intervalo $[-1, 1]$, podemos cambiarla multiplicando simplemente por un factor $A$.
$$A sin(\frac{2\pi}{L}x)$$
Del mismo modo podemos desplazar la función usando un offset. Normalmente este offset recibe el nombre de fase $\phi$.
La función seno "tuneada" nos queda:
$$A sin(\frac{2\pi}{L}(x + \phi))$$
El offset es perfecto para incluir desplazamientos debido a la velocidad:
$$ \phi = S t $$
Siendo $S$ la velocidad y $t$ el tiempo.
Un apunte importante es el siguiente: en UE4 cuando trabajamos con materiales la función seno tiene periodo $1$. A diferencia del seno matemático que tiene periodo $2\pi$.
Es decir, la fórmula anterior queda así usando la función $sin$ de UE4:
$$A sin_{ue4}(\frac{1}{L}(x + S t))$$
Vamos finalmente a implementarla en UE4:
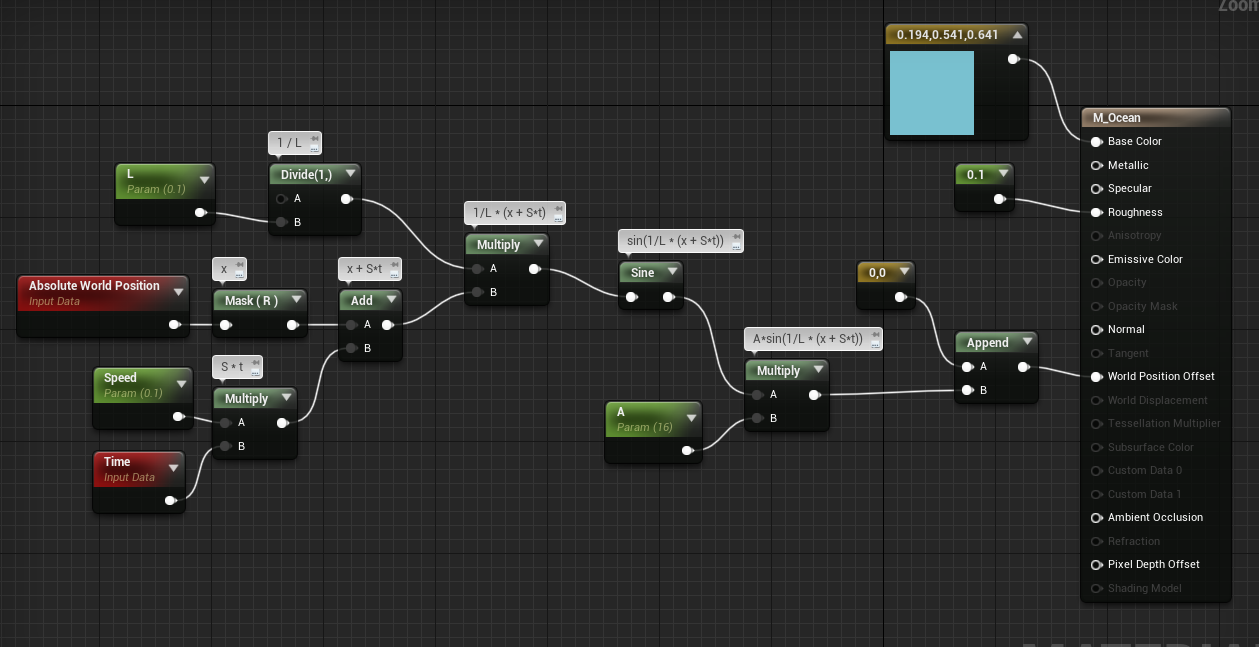

Buen comienzo.
En este ejemplo la dirección de movimiento es de izquierda a derecha. ¿Podemos hacer que se desplace de arriba a abajo?
Sería tan sencillo como cambiar la variable de entrada: $A sin(\frac{1}{L}(y + S t))$.
¿Y de mover de derecha a izquierda? $A sin(\frac{1}{L}(-x + S t))$
¿Y si queremos movernos de izquierda a derecha y de arriba a abajo? $A sin(\frac{1}{L}(x + y + S t))$
¿Y si queremos movernos el doble de rápido a la derecha que hacia abajo? $A sin(\frac{1}{L}(2x + y + S t))$
En general, si tenemos una dirección $D = (D_x, D_y)$ tenemos la siguiente fórmula:
$$ A sin(\frac{1}{L}(D_x x + D_y y + S t)) $$
Podemos compactar la expresión usando el producto escalar:
$$ A sin(\frac{1}{L}(D \cdot (x, y) + S t)) $$
El material modificado:
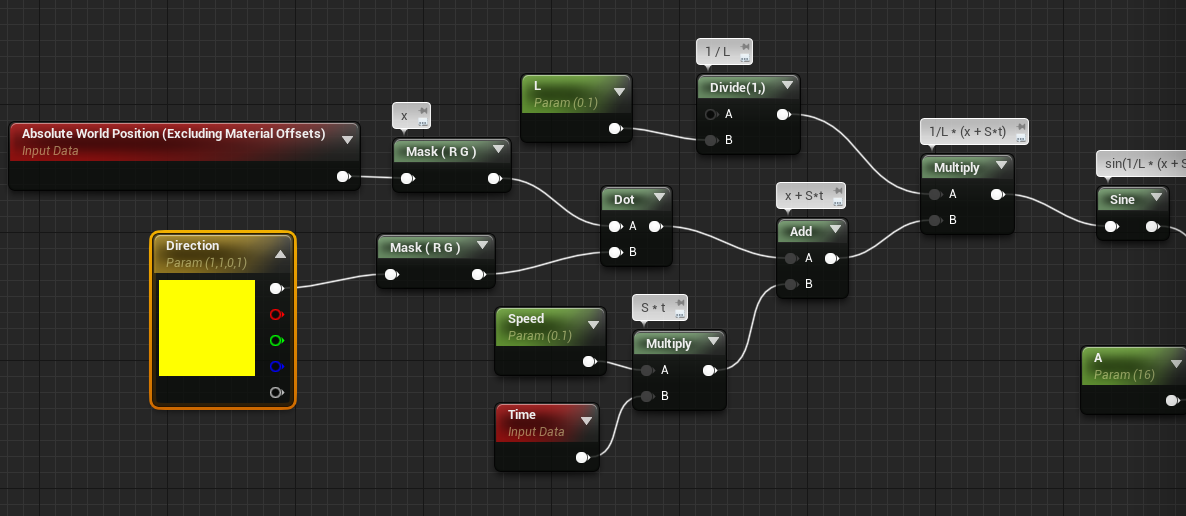

Como podrás comprobar este material carece de las normales, está usando las normales del grid.
Vamos a corregirlo.
Cálculo de las normales
Para calcular las normales de un material de manera dinámica en tiempo real existen multitud de técnicas. Desde usar las diferencias centrales finitas a usar las propiedades DDX y DDY del shader.
Sin embargo, dado que tenemos la fórmula analítica de la superficie, podemos calcular la normal de manera analítica y por tanto exacta.
Para calcular la normal $N$ de un punto $P$ de la superficie hacemos lo siguiente:
- Calcular una tangente $T$ en el punto $P$.
- Calcular una segunda tangente $B$ perpendicular a $T$ en el punto $P$.
- Por definición de producto vectorial, la normal $N$ es el producto vectorial de $T$ y $B$.
¿Cómo se calcula la tangente en un punto $P$ de una función? ¡La derivada!
La función es:
$$P(x, y) = (x, y, A sin(\frac{1}{L}(D \cdot (x, y) + S t))) $$
Como tenemos que calcular dos tangentes, digamos que $T$ es la tangente en dirección $x$ (derivada con respecto a $x$) y la tangente $B$ es la tangente en dirección $y$ (derivada con respecto a $y$).
$$ T(x,y) = \frac{\partial P(x,y)}{\partial x} = (\frac{\partial x}{\partial x}, \frac{\partial y}{\partial x}, \frac{\partial(A sin(\frac{1}{L}(D \cdot (x, y) + S t)))}{\partial x}) $$
$$ B(x,y) = \frac{\partial P(x,y)}{\partial y} = (\frac{\partial x}{\partial y}, \frac{\partial y}{\partial y}, \frac{\partial(A sin(\frac{1}{L}(D \cdot (x, y) + S t)))}{\partial y}) $$
Vamos a calcular para $T$:
$$ T(x,y) = \frac{\partial P(x,y)}{\partial x} = (\frac{\partial x}{\partial x}, \frac{\partial y}{\partial x}, \frac{\partial(A sin(\frac{1}{L}(D \cdot (x, y) + S t)))}{\partial x}) $$
$$ T(x,y) = (1, 0, \frac{\partial(A sin(\frac{1}{L}(D \cdot (x, y) + S t)))}{\partial x}) $$
La coordenada $z$:
$$ z = \frac{\partial(A sin(\frac{1}{L}(D \cdot (x, y) + S t)))}{\partial x} $$
Aplicando la regla de la cadena:
$$z = A cos(\frac{1}{L} (D \cdot p + S t)) \frac{\partial}{\partial x}(\frac{1}{L}(D \cdot p + S t))$$
$$z = \frac{A}{L} D_x cos(\frac{1}{L} (D \cdot p + S t)) $$
Por tanto nos queda:
$$ T(x,y) = (1, 0, \frac{A}{L} D_x cos(\frac{1}{L} (D \cdot p + S t))) $$
Y para la bitangente:
$$ B(x,y) = (0, 1, \frac{A}{L} D_y cos(\frac{1}{L} (D \cdot p + S t))) $$
Si hacemos el producto vectorial de ambos vectores:
$$ N = T \times B $$
Tenemos el siguiente resultado:
$$ N_x = -\frac{A}{L} D_x cos(\frac{1}{L} (D \cdot p + S t)) $$
$$ N_y = -\frac{A}{L} D_y cos(\frac{1}{L} (D \cdot p + S t)) $$
$$ N_z = 1 $$
Que nos da las normales de la superficie:

Puedes hacer los cálculos usando los nodos del material editor tal y como hemos hecho anteriormente.
En este caso, en cambio, he preferido usar HLSL por comodidad:
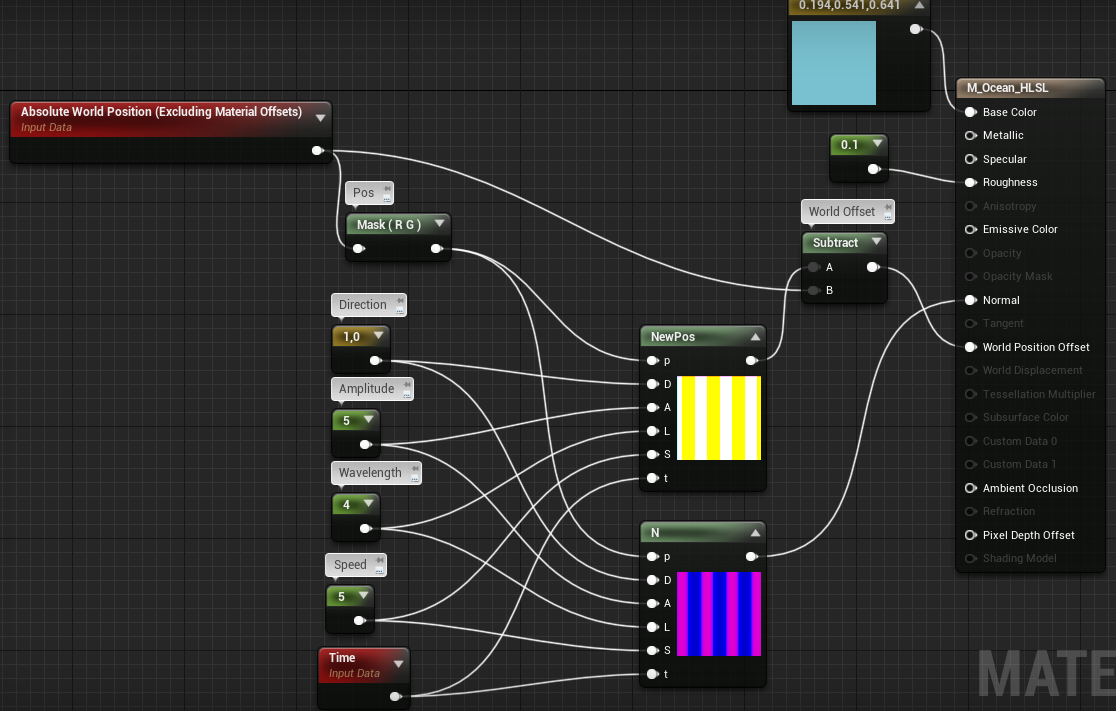
Dónde el CustomNode llamado NewPos tiene el siguiente código:
float k = 1.0 / L;
float z = A * sin(k * ( dot(p, D) + S * t ));
return float3(p.x, p.y, z);Y el nodo CustomNode llamado N para calcular la normal tiene el siguiente código:
float k = 1.0 / L;
float Nx = A * k * D.x * cos(k * ( dot(p, D) + S * t ));
float Ny = A * k * D.y * cos(k * ( dot(p, D) + S * t ));
return normalize(float3(-1. * Nx, -1. * Ny, 1.0));Nota: en HLSL las funciones trigonométricas seno y coseno sí tienen periodo $2\pi$ a diferencia de los nodos seno y coseno normalizados del editor de materiales. He mantenido la misma constante $k$ por simplicidad. Solo afecta a la magnitud que demos a los valores de $S$ y $D$.
Suma de senos
Hasta ahora estamos usando una simple función seno, pero un océano es una "suma" de muchos movimientos ondulatorios. ¡Vamos a usar muchos senos!
Podríamos empaquetar la función en un material function y llamarla multitud de veces y sumar el resultado.
En mi caso, voy a reemplazar el código anterior y sumaré multitud de senos cada uno con distintos parámetros dados en un array:
int Num = 3;
float AA[] = {5.0, 2.0, 12.0};
float LL[] = {4.0, 6.0, 8.0};
float SS[] = {5.0, 8.0, 2.0};
float2 DD[] = {{1.0, 0.0}, {0.3, 0.8}, {0.9, -0.1}};
float z = 0.0;
for (int i = 0; i < Num; ++i)
{
float A = AA[i];
float L = LL[i];
float S = SS[i];
float2 D = DD[i];
float k = 1.0 / L;
z += A * sin(k * ( dot(p, D) + S * t ));
}
z = z / Num;
return float3(p.x, p.y, z);int Num = 3;
float AA[] = {5.0, 2.0, 12.0};
float LL[] = {4.0, 6.0, 8.0};
float SS[] = {5.0, 8.0, 2.0};
float2 DD[] = {{1.0, 0.0}, {0.3, 0.8}, {0.9, -0.1}};
float Nx = 0.0, Ny = 0.0;
for (int i = 0; i < Num; ++i)
{
float A = AA[i];
float L = LL[i];
float S = SS[i];
float2 D = DD[i];
float k = 1.0 / L;
Nx += A * k * D.x * cos(k * ( dot(p, D) + S * t ));
Ny += A * k * D.y * cos(k * ( dot(p, D) + S * t ));
}
Nx = Nx / Num;
Ny = Ny / Num;
return normalize(float3(-Nx, -Ny, 1.0));Que nos da resultados muy interesantes y bastante aproximados a un océano tranquilo:

Modificando el seno
El problema con la función seno es que es demasiado "suave". Sube y baja de manera contínua a la misma velocidad. Mientras que una ola en la vida real su cresta es mucho más aguda.
Un truco podría ser elevar a una potencia la función seno. Por ejemplo la siguiente gráfica:
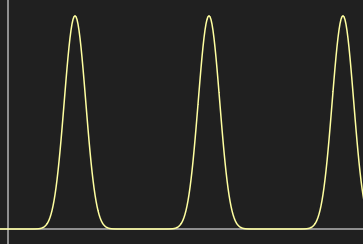
Corresponde a la función:
$$ f(x) = (sin(x))^{16}$$
También podemos usar la función exponencial:
$$ f(x) = e^{sin(x) - 1} $$
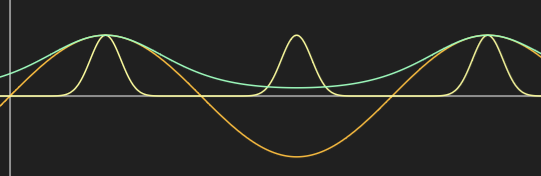
Mucho más aproximada a una ola real. Tendríamos que recalcular las normales.
Esta sería una aproximación completamente válida y mejoraría nuestra primera iteración.
Vamos a ilustrarlo usando:
$$P(x, y) = (x, y, e^{sin(g) - 1})$$
Con $g$ siendo la función que vimos anteriormente:
$$g = \frac{1}{L} D \cdot (x, y) + S t$$
La derivada para calcular las normales es trivial habiendo calculado, como hemos hecho anteriormente, la derivada de $g$.

Anteriormente hemos usado arrays para sumar las distintas ondas.
En este caso vamos a generar proceduralmente, y de forma completamente arbitraria, los distintos parámetros para cada onda:
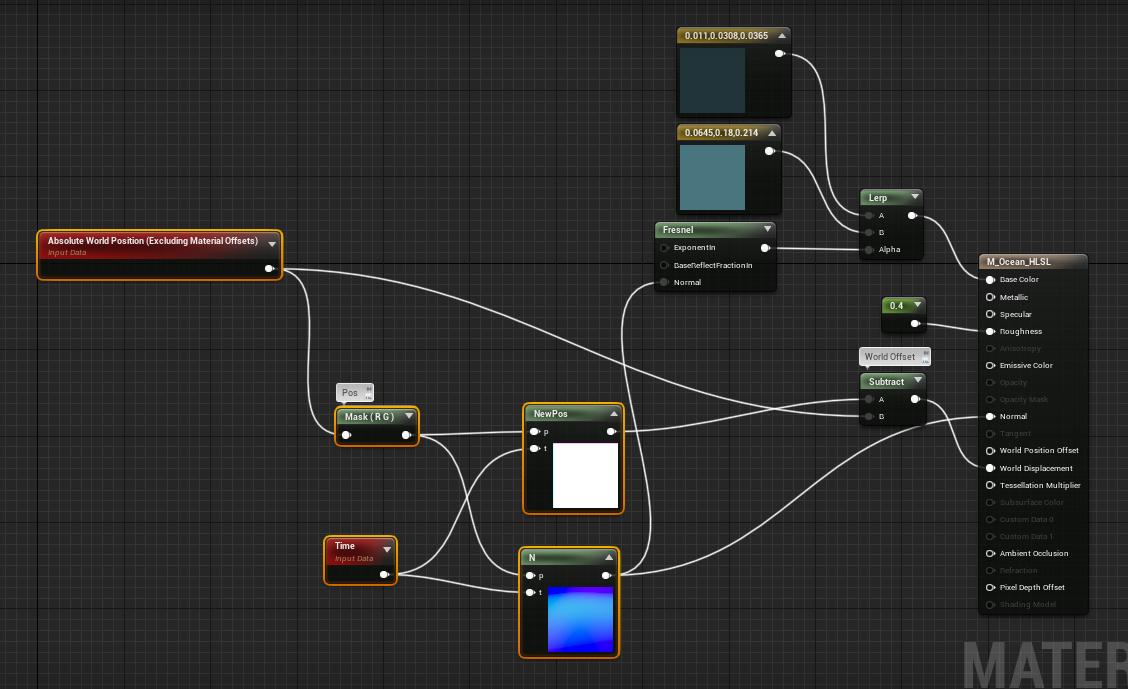
En este caso el nodo NewPos contiene el siguiente código:
int Num = 20;
float A = 16.0;
float iter = 0.0;
float S = 12.0;
float L = 16.0;
float z = 0.0;
for(int i = 0; i < Num; i++){
float2 D = float2(sin(iter), cos(iter));
// calculate wave
float k = 1.0 / L;
float wave = A * exp(sin(k * ( dot(p, D) + S * t )) - 1);
//
z += wave;
iter += 4.0;
A *= 0.6;
L *= 1.18;
S *= 1.07;
}
return float3(p.x, p.y, z);Y el nodo N el siguiente código:
int Num = 20;
float A = 16.0;
float iter = 0.0;
float S = 12.0;
float L = 16.0;
float Nx = 0.0, Ny = 0.0;
for(int i = 0; i < Num; i++){
float2 D = float2(sin(iter), cos(iter));
// calculate wave
float k = 1.0 / L;
float wave = A * exp(sin(k * ( dot(p, D) + S * t )) - 1);
Nx += wave * A * k * D.x * cos(k * ( dot(p, D) + S * t ));
Ny += wave * A * k * D.y * cos(k * ( dot(p, D) + S * t ));
//
iter += 4.0;
A *= 0.6;
L *= 1.18;
S *= 1.07;
}
Nx = Nx / Num;
Ny = Ny / Num;
return normalize(float3(-Nx, -Ny, 1.0));Alterando la "forma" de la función seno podemos aproximarnos mucho a la forma final de un océano.
Gerstner Waves
Sin embargo, por mucho que alteremos la función seno tenemos un error fatal en nuestro diseño. Solo nos movemos en el eje Z.
En la vida real, las partículas de agua no solo se mueven arriba abajo, en el eje Z, sino también hacía adelante y hacía atrás, eje X, ocupando el espacio de sus partículas vecinas.
Este comportamiento fue estudiado por un señor de apellido Gerstner. También llamada onda Trochoidal.
La onda de Gerstner u onda Trochoidal es solución a la ecuación de Euler para superficies ondulatorias afectadas por la gravedad.
La idea intuitiva es que las partículas se mueven siguiendo una circunferencia:
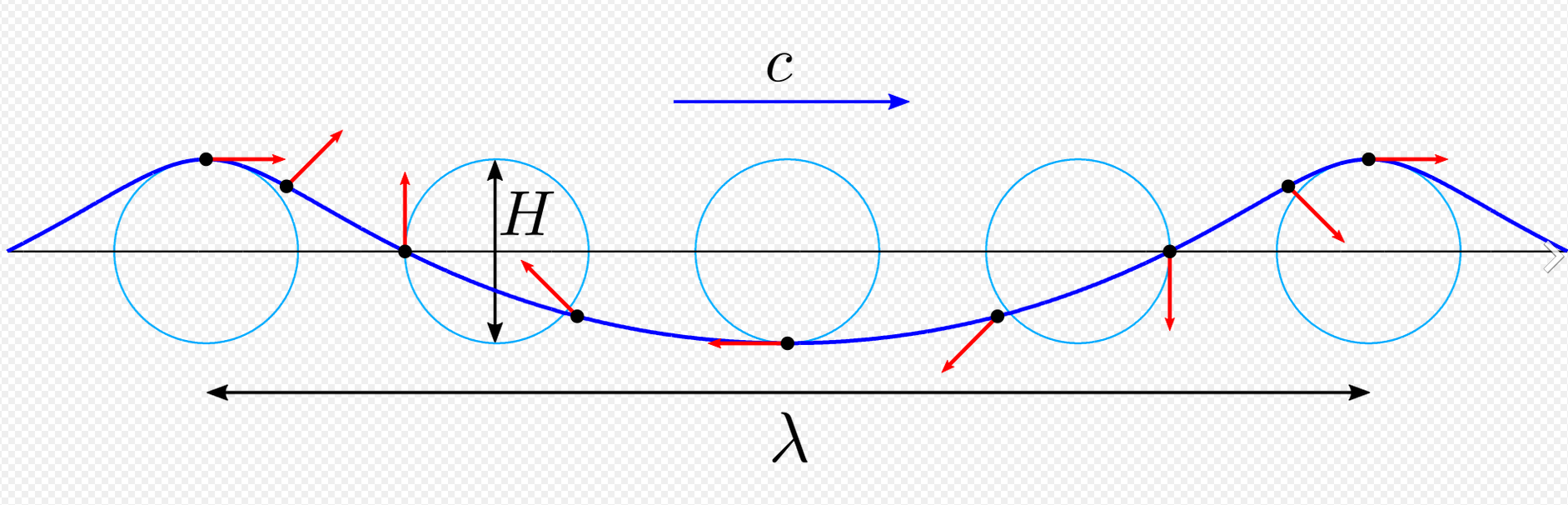
La ecuación de una circunferencia cuyo punto de anclaje (anchor point) es $(C_x, C_y)$ es:
$$\zeta(x, y) = (C_x + cos(x), C_y + sin(x))$$
¿Cómo lo aplicamos a nuestro original $P(x, y)$? En nuestra versión original solo modificamos la coordenada z.
En esta versión modificada usando Gerstner además modificamos las coordenadas x e y siguiendo la circunferencia.
Veamos como quedaría la coordenada x modificada. Mismo razonamiento para y.
$$ P_x = C_x + A cos(\frac{1}{L} (D \cdot (x, y) + S t)) $$
Simplemente hemos añadido el desplazamiento siguiendo la circunferencia.
¿Qué valor tiene $C_x$? Precisamente usamos como anchor point la posición del grid. Por lo que $C = (C_x, C_y) = (x, y)$:
$$P_x = x + A cos(\frac{1}{L} (D \cdot (x, y) + S t))$$
Por último, no hay que olvidar que al movernos arbitrariamente por cualquier dirección $D$, el desplazamiento en x debe estar modulado por $D$:
$$P_x = x + A D_x cos(\frac{1}{L} (D \cdot (x, y) + S t))$$
También nos gustaría tener cierto control artístico y poder controlar "cuanto" desplazamiento lateral ocurre. Para ello introducimos un nuevo parámetro $Q$ para controlar precisamente el desplazamiento lateral.
$$P_x = x + Q A D_x cos(\frac{1}{L} (D \cdot (x, y) + S t))$$
Este desplazamiento lateral es responsable, en última instancia, de como de "aguda" es la cresta de la ola:
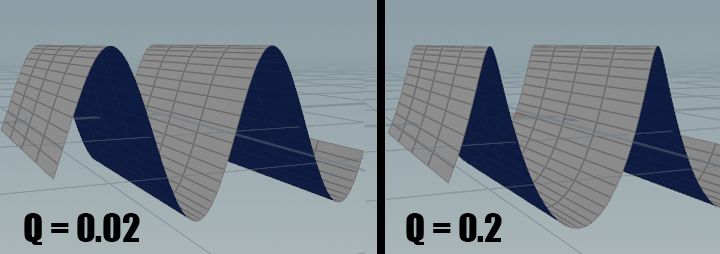
Hay que tener precaución ya que para valores de $Q$ suficientemente altos puede ocurrir que el desplazamiento lateral rompa la ola:

Las ecuaciones finales son:
$$P_x = x + Q A D_x cos(\frac{1}{L} (D \cdot (x, y) + S t))$$
$$P_y = y + Q A D_y cos(\frac{1}{L} (D \cdot (x, y) + S t))$$
$$P_z = A sin(\frac{1}{L} (D \cdot (x, y) + S t)) $$
Si calculamos las derivadas para obtener $T$ y $B$ para posteriormente hacer el producto vectorial y finalmente conseguir la normal $N$ tenemos:
$$ N_x = -\frac{1}{L} A D_x cos(\frac{1}{L} (D \cdot (x, y) + S t)) $$
$$ N_y = -\frac{1}{L} A D_y cos(\frac{1}{L} (D \cdot (x, y) + S t)) $$
$$ N_z = 1 -\frac{1}{L} Q A sin(\frac{1}{L} (D \cdot (x, y) + S t)) $$
Y aquí el código para calcular la posición y la normal:
float2 D = {1, 1};
float A = 100.0;
float L = 90.0;
float S = 120.0;
float Q = 0.2;
float w = 1.0 / L;
p.x = p.x + Q * A * D.x * cos(w * (dot(D, p) + S * t));
p.y = p.y + Q * A * D.y * cos(w * (dot(D, p) + S * t));
p.z = A * sin(w * (dot(D, p) + S * t));
return p;
float2 D = {1, 1};
float A = 100.0;
float L = 90.0;
float S = 120.0;
float Q = 0.2;
float w = 1.0 / L;
float WA = w * A;
float S_ = sin(w * (dot(D, p) + S * t));
float C_ = cos(w * (dot(D, p) + S * t));
float3 NN;
NN.x = -D.x * WA * C_;
NN.z = -D.y * WA * C_;
NN.y = 1.0 - Q * WA * S_;
return normalize(NN);
Antes de hacer la suma de ondas tal y como hicimos con el seno, vamos a quitarnos el parámetro velocidad que será controlado por la longitud de onda.
Longitud de onda y velocidad
Físicamente la velocidad de una onda de Gerstner bajo los efectos de la gravedad está en función de la longitud de onda.
Cuanta mayor longitud de onda más rápidamente se mueve y al contrario, cuando mejor longitud de onda más lento es su movimiento.
En concreto, en las referencias que acompaña este artículo puedes encontrar la fórmula de la velocidad:
$$S = \sqrt{\frac{g L}{2 \pi}}$$
Dónde $g$ es la aceleración de la gravedad: $9,8$. En UE4 se trabaja con centímetros así que este valor $g = 980$.
Forma general del océano
Si sumamos, al igual que hicimos con seno, las ondas Gerstner tenemos la forma general del océano.
En primera instancia, para organizarnos, he creado varios material function. Uno para el cálculo de la nueva posición y otra para el cálculo de la derivada.
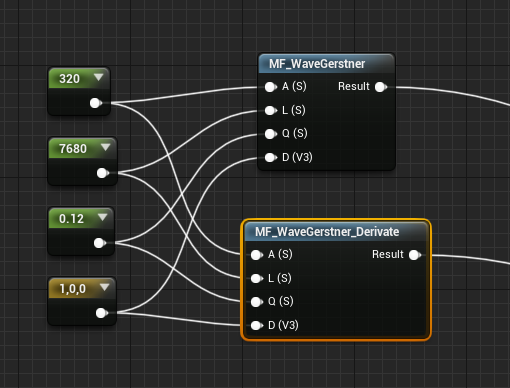
Dónde el material function no es más que un nodo Custom Node con el código HLSL anterior.
Si sumamos varias ondas cada una con distintos parámetros:
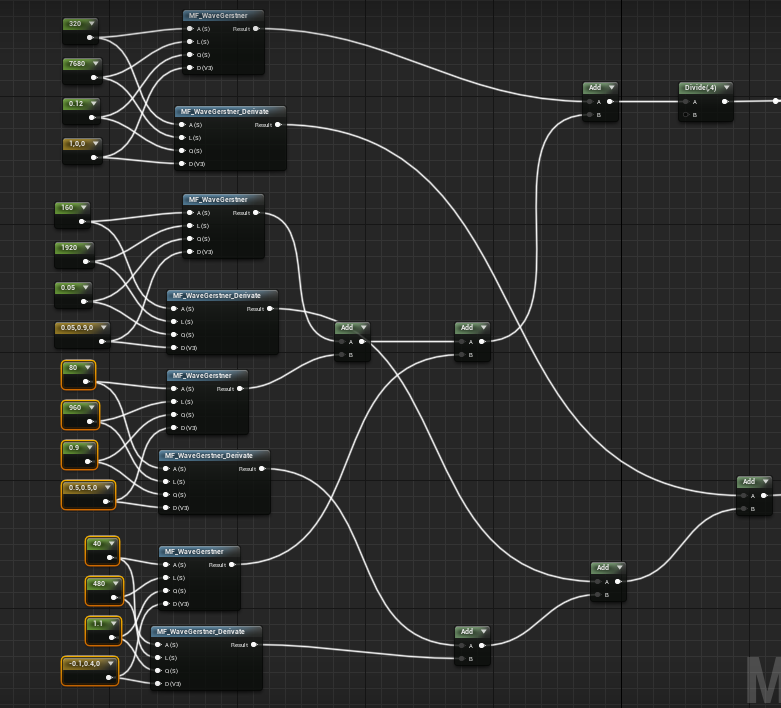
Tenemos la forma general del océano.
Para el color, podemos hacer un gradiente en función de la altura de la ola. Para ello usamos la posición Z del fragmento:
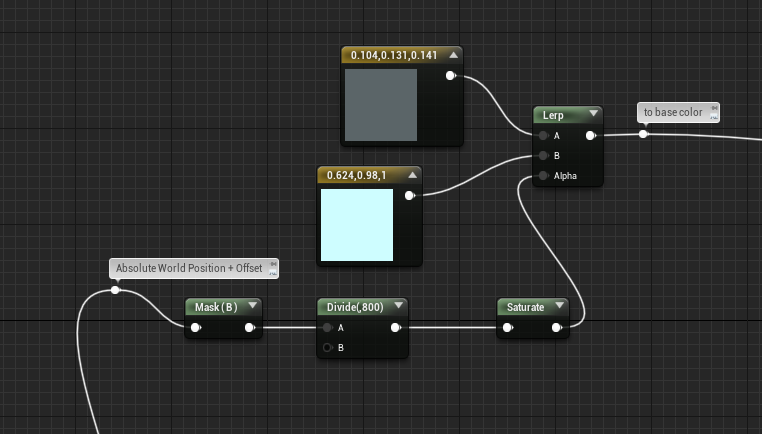
Obteniendo el siguiente resultado:

Añadir detalles
Podemos añadir detalles usando mapas de normales de agua.
Puedes descargar algunos de aquí:

Para darle sensación de movimiento puedes panear doblemente la textura y sumar las normales.
¿Qué coordenadas UV usamos para indexar la textura? Puedes usar planar projection. Aquí hay un post sobre ello.
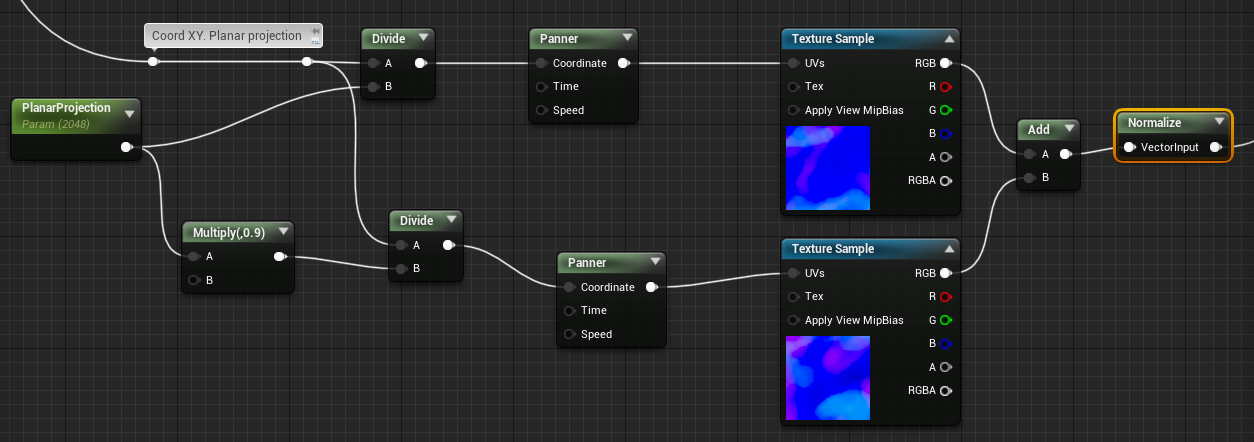
Si sumamos estas normales con las normales que calculamos de la suma de ondas Gerstner tenemos:

Especular
Podemos usar el cálculo típico para la componente especular:
// Código genérico para el cálculo básico de la componente especular
float specularStrength = 0.5;
vec3 viewDir = normalize(viewPos - FragPos);
vec3 reflectDir = reflect(-lightDir, norm);
float spec = pow(max(dot(viewDir, reflectDir), 0.0), 32);Más información en este estupendo post sobre iluminación básica.
En UE4 sería:

Puedes jugar también con el fresnel para añadirlo al emissivo junto al especular.
El resultado:

Resultado final
El resultado final:

Referencias






