Cuando en una cámara inciden 3 fotones, el sensor recoge 3 fotones, si inciden 6 fotones, el sensor recoge 6. Hay una relación lineal. Sin embargo el ojo humano no funciona así, ve las imágenes más brillantes de lo que realmente son (es decir, "ve" más fotones de los que realmente han incidido) en una relación no lineal:
$$V_{out} = V_{in} ^ \gamma$$
Más ilustrativo en esta gráfica:
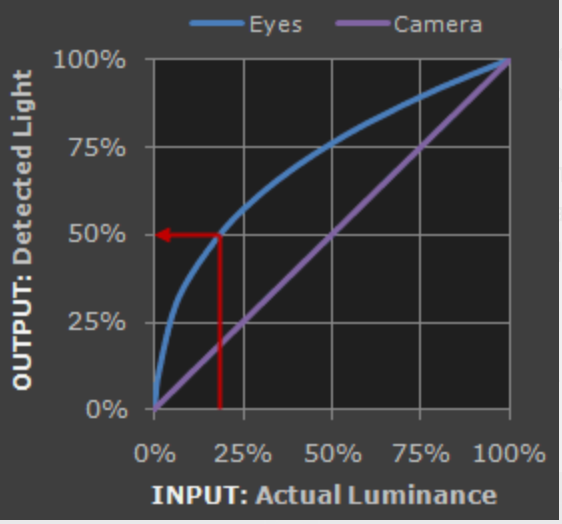
Es decir, el ojo humano tiene un valor $\gamma$ (gamma) distinto de 1 que provoca esa no-linealidad.
De hecho, comparado con una cámara, el ojo es mucho más sensible a cambios entre tonalidades negras que entre tonalidades brillantes (tiene su explicación biológica) como se puede comprobar en la gráfica anterior.
Por ese motivo, se codifican las imágenes con gamma. Pero ¿qué significa codificar con gamma?
Si codificamos la imagen con, por ejemplo, 5 bits ($2^5 = 32$ valores) de información y almacenáramos la imagen de forma lineal (curva morada de la gráfica anterior) estaríamos asignando 16 valores a los tonos más oscuros y 16 valores a los tonos más brillantes.
Asignar de esta manera es un completo desperdicio porque (mirando la gráfica) el ojo humano casi no diferencia entre tonos más brillantes y sí diferencia entre tonos más oscuros.
Es decir, estamos asignando 16 valores para codificar los tonos más brillantes y 16 los más oscuros cuando el ojo humano es muy bueno diferenciando los tonos oscuros (¡necesitamos más de 16 valores!) y muy malo diferenciando los tonos claros (¡nos sobra 16 valores!).
Tiene sentido, por tanto, asignar más bits de información para codificar los tonos oscuros que los brillantes.
Esto es, precisamente, lo que se consigue con la curva gamma (línea azul en la gráfica superior) de manera que los bits se distribuyen más en los tonos oscuros (hay más bits para codificar tonos oscuros) y menos en los claros.
Ahora está el problema de visualizar la imagen que hemos codificado con gamma. El ojo tiene que ver la línea morada de la gráfica para "convertirla" de modo natural en la azul (el ojo tiene su propio gamma). Por tanto, el dispositivo reproductor (el monitor o la tv) tiene que cancelar el gamma de la imagen codificada.
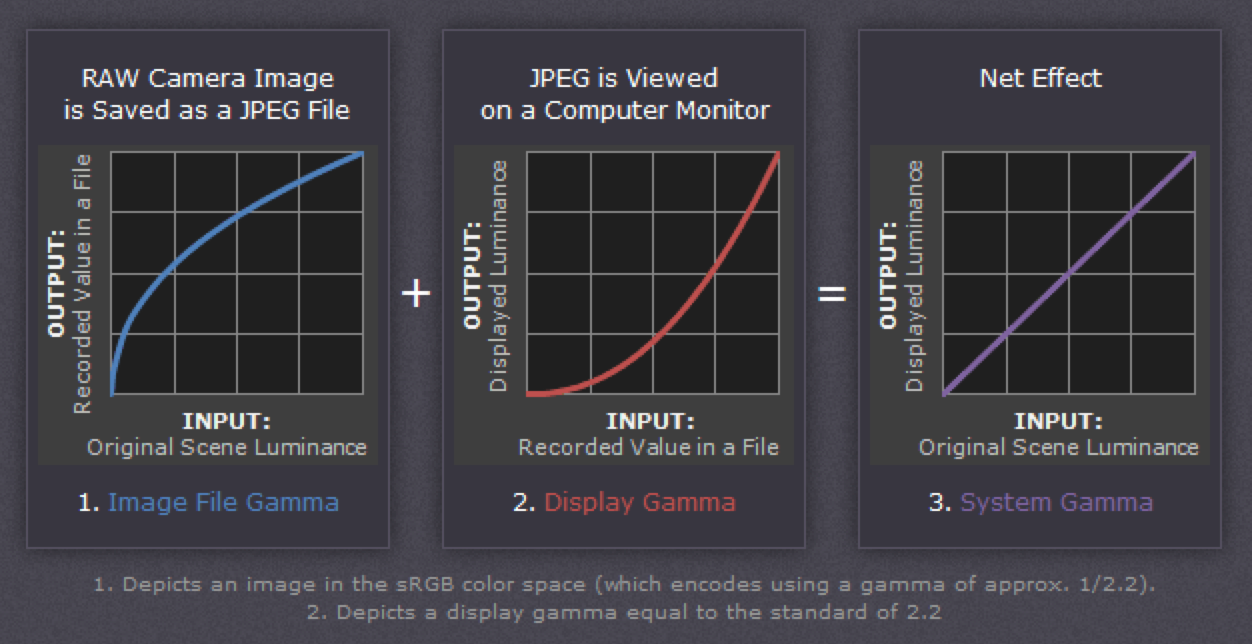
Por cierto, no es cierto que este proceso se desarrollara para compensar las características de entrada/salida de los monitores CRT.
Todo este proceso es automático.
Y llegados a este punto y sabiendo que este proceso es automático ¿qué $#@! importa para desarrollar videojuegos? Pues mucho, en concreto, al calcular la luz.
Toma el siguiente fragment shader clásico:
float specular = ...;
float3 color = tex2D(samp,uv.xy);
float diffuse = saturate(dot(N,L));
float3 finalColor = color * diffuse + specular;
return finalColor;¿Y qué hay de malo?
Pues que al leer la textura directamente está usando una información de color incorrecta.
¿Por qué es incorrecta? Recuerda que la textura está gamma-codificada, es decir, es mucho más brillante y más desaturada que como la verías en tu monitor (porque el monitor aplicaría un gamma $2.2$ al mostrarla) y con esa imagen gamma-codificada es con la que haces los cálculos de luz, y después de eso, al salir en la TV se aplica el gamma automática de TV.
Esto es erróneo porque se está haciendo los cálculos de luz con texturas que no son las que se van a ver, no son el color correcto (las que se van a ver tienen un gamma aplicado por parte del monitor de 2.2).
¿Y cómo se arregla? Hay que hacer los cálculos de luz con el color correcto que va a ver el jugador. Aquí el shader modificado:
float specular = ...;
float3 color = pow(tex2D(samp,uv.xy),2.2);
float diffuse = saturate(dot(N,L));
float3 finalColor = pow(color * diffuse + specular,1/2.2);
return finalColor;Esos pow no son "gratis" en los shaders (que se ejecutan millones de veces) por lo que el impacto en rendimiento no es despreciable.
Sin embargo, podemos activar dos flags en los "hardware sampler states" en las tarjetas gráficas compatibles (no todas los son, por ejemplo no lo son en los móviles antiguos).
Los flags en cuestión son SRGBTEXTURE y SRGBWRITEENABLE y por tanto el código quedaría exactamente como el primer shader y los pow serían gratis. Esto es lo que precisamente ocurre cuando en Unity cambias el color space de gamma a linear.
HDR (High Dynamic Range) y Tonemapping
Hasta ahora hemos hablado de que el ojo humano es más sensible a cambios entre tonalidades oscuras que entre tonalidades brillantes, por eso se dedican más bit de información a codificar los tonos oscuros que los brillantes siguiendo una curva $V_{out}=V_{in}^{gamma}$, es lo que hemos llamado codificación gamma. Sin embargo hay otra particularidad del ojo y es su comportamiento dinámico.
Vamos a ilustrarlo con un ejemplo:
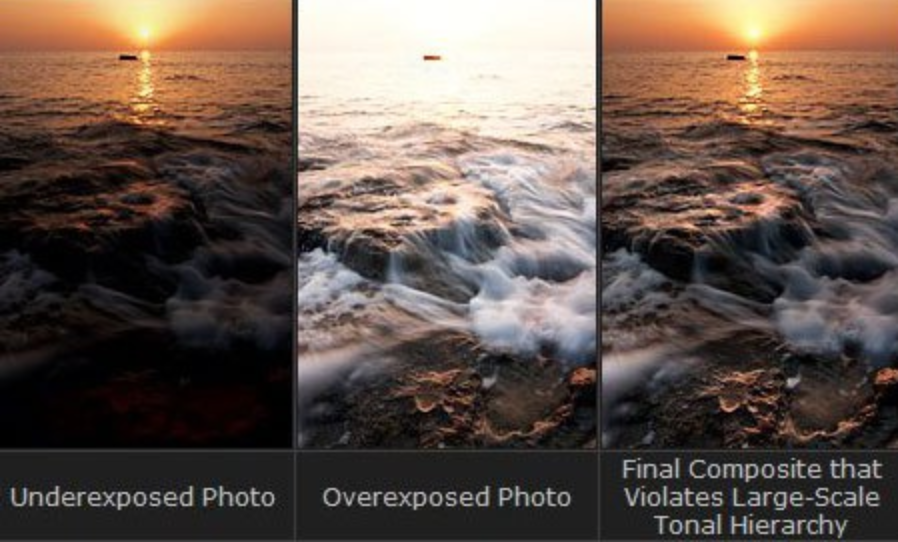
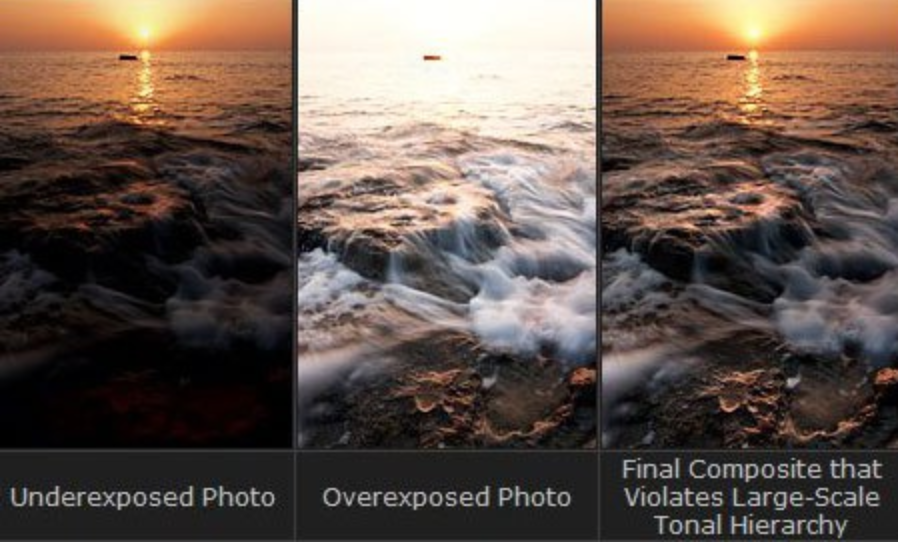
Si tienes 5 bits de información en una cámara el rango estático, tienes 32 valores para codificar, de 0 a 32, ahora falta decir ¿que cantidad de brillo corresponde al valor 32 y cuanto al valor 0? Es importante definirlos porque si el 0 es nada de brillo y el 32 máximo brillo perderás muchos detalles en la imagen (piensa en una imagen ultrarealista convertirla a una paleta de 32 colores).
En el ejemplo, si el 32 es máximo brillo y el 0 es algo menos de brillo entonces obtendrás todos los detalles de las zonas brillantes (ver imagen de la izda, underexposed) a costa de no diferenciar nada de las zonas oscuras. Por el contrario si 0 es nada de brillo y 32 es un poquito de brillo obtendrás todos los detalles de las zonas oscuras (ver imagen central, overexposed) a costa de no diferenciar detalles en las zonas brillantes.
Pero... En la vida real el ojo es capaz de enfocar las dos zonas, ¿que rango usa el ojo? Pues la clave aquí es que el ojo, aparte de usar muchísimos "bits" de información, tiene un rango dinámico: Es capaz de ajustar su rango en función de las condiciones de luz.
Es decir, cuando el ojo se fija en la zona brillante (parte superior de la imagen de arriba) asigna el valor 32 a máximo brillante y 0 a brillante obteniendo todos los detalles y cuando enfoca a la zona de oscura de abajo cambia el mapeo de valores y 32 es poco brillante y 0 nada brillante. Por ello cuando salimos de una habitación oscura a pleno sol tardamos un poco en ver con claridad.
¿Podemos crear una imagen en la que se pueda diferenciar todos los detalles (cambios de brillo)? Sí, y tanto la imagen como la técnica para crear dicha imagen se llama HDR. Con HDR se combinan las dos imágenes (izda y central) para crear la imagen de la derecha y básicamente actuan inspiradas en el ojo humano, según la región de la imagen el valor X puede significar un brillo distinto (rango dinámico).
En videojuegos lo que se hace es usar el doble de bits para almacenar el color. Algo así como cambiar un float por un double. Si se usan 8 bits para sRGB, cuando se activa HDR se pasa a usar sRGB 16 bits. Todos los cálculos de luz se hacen con 16 bits de información frente a los 8 bits que se usarían si no estuviera HDR activado.
Pero ahora tenemos un problema, los monitores y dispositivos de salida solo son capaces de mostrar 8 bits de luz, pero al activar HDR hacemos cálculo de 16 bits, ¿como presentamos cálculos de 16 bits en 8 bits? Es decir, ¿como mapeamos colores de 16 bits a 8? El proceso de mapear colores de HDR a LDR (low dynamic range) es llamado Tonemapping.
En UE4 puedes configurar el Tonemapping bajo la pestaña del mismo nombre en el Postprocess Volume.
Si no activas Tonemapping la conversión a LDR se hará de todas formas pero se hará "truncando" los valores (algo así como castear a float un double) por lo que es posible que se pierdan muchos detalles.
Algunos efectos funcionan realmente bien con HDR como es el caso de Bloom que además funciona bastante bien en combinación con Tonemapping.
Referencias
Algunas referencias interesantes:
Curva para Filmic Tonemapper de UE4
Documentación oficial de UE4 para Tonemapper
Documentación oficial de UE4 para HDR
Créditos
Gran parte de este post está inspirado de esta charla en la GDC. Algunas imágenes han sido tomadas de ahí.